Skip to main content

🟩 Binary Tree Inorder Traversal (#94)

🔗 Problem Link​

📋 Problem Statement​

You are given the root of a binary tree, return the inorder traversal of its nodes' values.

💡 Examples​

Example 1​

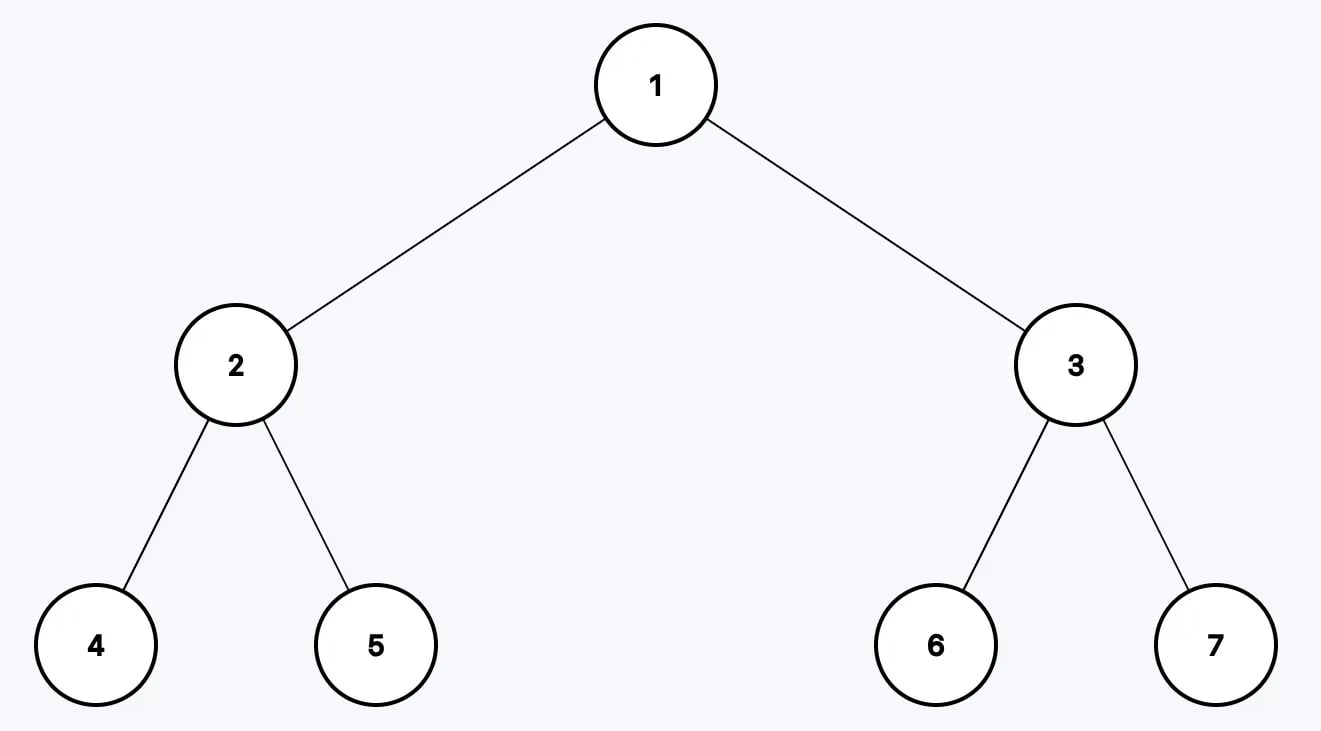
Binary Tree Inorder Traversal Example 1

Input: root = [1,2,3,4,5,6,7]
Output: [4,2,5,1,6,3,7]

Example 2​

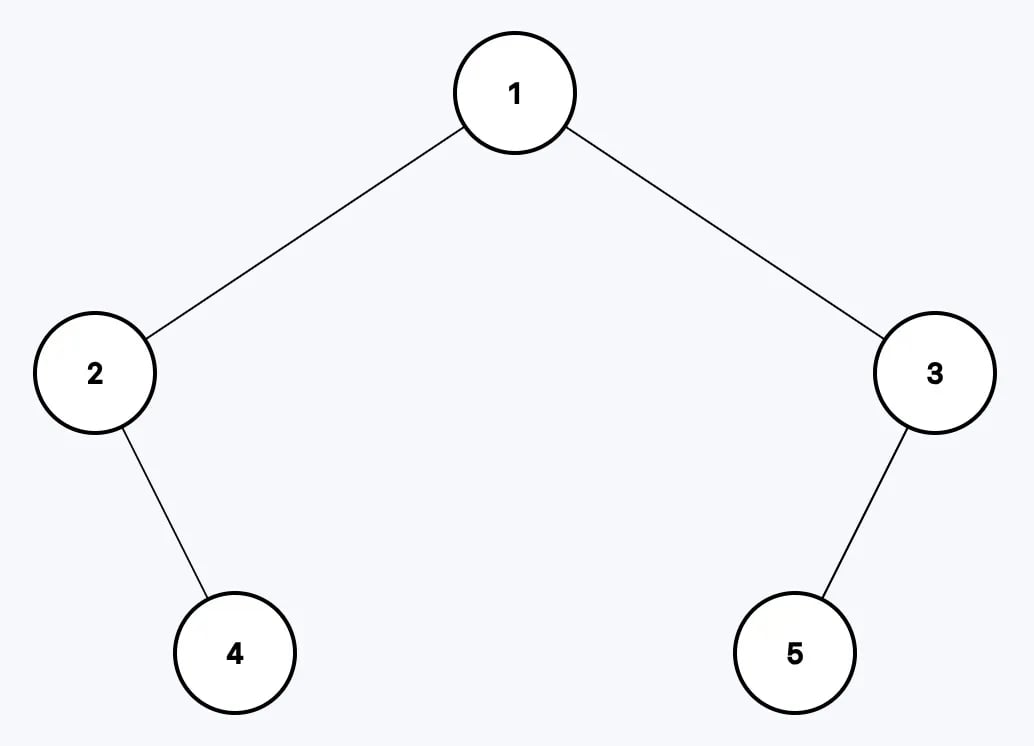
Binary Tree Inorder Traversal Example 2

Input: root = [1,2,3,null,4,5,null]
Output: [2,4,1,5,3]

Example 3​

Input: root = []
Output: []

🔑 Key Insights & Approach​

Core Observation: Inorder traversal visits nodes in a specific order: Left subtree → Root → Right subtree. This produces values in sorted order for a Binary Search Tree (BST).

Why Inorder Traversal?

  • Left-Root-Right: Process left child, then current node, then right child
  • Sorted output for BST: Values appear in ascending order
  • Two main approaches: Recursive (natural) vs Iterative (uses explicit stack)

The Mental Model: Think of reading a book: you first read the left pages (left subtree), then the spine/center (root), then the right pages (right subtree). This naturally gives you the "inorder" reading.

Recursive Approach:

  1. Recursively traverse left subtree
  2. Visit current node (add to result)
  3. Recursively traverse right subtree

Iterative Approach (Using Stack):

  1. Go as far left as possible, pushing nodes onto stack
  2. When can't go left anymore, pop from stack and visit node
  3. Move to right child and repeat

Why Two Approaches?

  • Recursive: Clean and intuitive, matches the definition directly
    • Time: O(n), Space: O(h) where h is tree height (call stack)
  • Iterative: More explicit, avoids recursion overhead
    • Time: O(n), Space: O(h) (explicit stack instead of call stack)

Pattern Recognition: This is the "Tree Traversal" pattern. Inorder is one of three DFS traversals (Preorder: Root-Left-Right, Inorder: Left-Root-Right, Postorder: Left-Right-Root).

🐍 Solution: Python​

Approach 1: Recursive​

Time Complexity: O(n) | Space Complexity: O(h) where h is tree height

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

def inorderTraversal(root: Optional[TreeNode]) -> List[int]:
    result = []

    def inorder(node):
        if not node:
            return

        # Left -> Root -> Right
        inorder(node.left)      # Traverse left subtree
        result.append(node.val)  # Visit root
        inorder(node.right)      # Traverse right subtree

    inorder(root)
    return result

Approach 2: Iterative with Stack​

Time Complexity: O(n) | Space Complexity: O(h)

def inorderTraversal(root: Optional[TreeNode]) -> List[int]:
    result = []
    stack = []
    current = root

    # Continue while there are nodes to process
    while current or stack:
        # Go as far left as possible
        while current:
            stack.append(current)
            current = current.left

        # Process node (no more left children)
        current = stack.pop()
        result.append(current.val)

        # Move to right subtree
        current = current.right

    return result

Approach 3: Morris Traversal (Advanced)​

Time Complexity: O(n) | Space Complexity: O(1) - No stack or recursion!

def inorderTraversal(root: Optional[TreeNode]) -> List[int]:
    result = []
    current = root

    while current:
        if not current.left:
            # No left child, visit and go right
            result.append(current.val)
            current = current.right
        else:
            # Find inorder predecessor (rightmost node in left subtree)
            predecessor = current.left
            while predecessor.right and predecessor.right != current:
                predecessor = predecessor.right

            if not predecessor.right:
                # Create thread to current node
                predecessor.right = current
                current = current.left
            else:
                # Thread already exists, remove it
                predecessor.right = None
                result.append(current.val)
                current = current.right

    return result

🔵 Solution: Golang​

Approach 1: Recursive​

Time Complexity: O(n) | Space Complexity: O(h)

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

func inorderTraversal(root *TreeNode) []int {
    result := []int{}

    var inorder func(*TreeNode)
    inorder = func(node *TreeNode) {
        if node == nil {
            return
        }

        // Left -> Root -> Right
        inorder(node.Left)
        result = append(result, node.Val)
        inorder(node.Right)
    }

    inorder(root)
    return result
}

Approach 2: Iterative with Stack​

Time Complexity: O(n) | Space Complexity: O(h)

func inorderTraversal(root *TreeNode) []int {
    result := []int{}
    stack := []*TreeNode{}
    current := root

    for current != nil || len(stack) > 0 {
        // Go as far left as possible
        for current != nil {
            stack = append(stack, current)
            current = current.Left
        }

        // Process node
        current = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        result = append(result, current.Val)

        // Move to right subtree
        current = current.Right
    }

    return result
}

Approach 3: Morris Traversal​

Time Complexity: O(n) | Space Complexity: O(1)

func inorderTraversal(root *TreeNode) []int {
    result := []int{}
    current := root

    for current != nil {
        if current.Left == nil {
            // No left child, visit and go right
            result = append(result, current.Val)
            current = current.Right
        } else {
            // Find inorder predecessor
            predecessor := current.Left
            for predecessor.Right != nil && predecessor.Right != current {
                predecessor = predecessor.Right
            }

            if predecessor.Right == nil {
                // Create thread
                predecessor.Right = current
                current = current.Left
            } else {
                // Remove thread
                predecessor.Right = nil
                result = append(result, current.Val)
                current = current.Right
            }
        }
    }

    return result
}

📚 References​